Nota Técnica

El costo oculto del FEM: Cuándo debes buscar una alternativa

septiembre 3, 2025

1. Resumen ejecutivo

El Método de los Elementos Finitos (FEM) es la técnica de simulación de referencia en la ingeniería mecánica para el análisis del comportamiento de productos y estructuras.¹ No obstante, a pesar de su versatilidad, el FEM presenta limitaciones notables al abordar ciertos fenómenos físicos, como el flujo de fluidos, las grandes deformaciones o los dominios de análisis semiinfinitos. Esta complejidad inherente de los problemas del mundo real ha impulsado el desarrollo de métodos numéricos alternativos y altamente especializados. Este informe presenta un análisis comparativo de estas alternativas, incluyendo el Método de los Volúmenes Finitos (FVM), el Método de los Elementos de Contorno (BEM) y los Métodos sin Malla, como el de Hidrodinámica de Partículas Suavizadas (SPH) y el de Elementos Discretos (DEM). Se discuten sus principios, ventajas y desventajas, destacando la creciente tendencia hacia los enfoques híbridos. Finalmente, se exploran las futuras líneas de investigación, como la computación cuántica y la inteligencia artificial, que prometen transformar la simulación de ingeniería.

2. Introducción

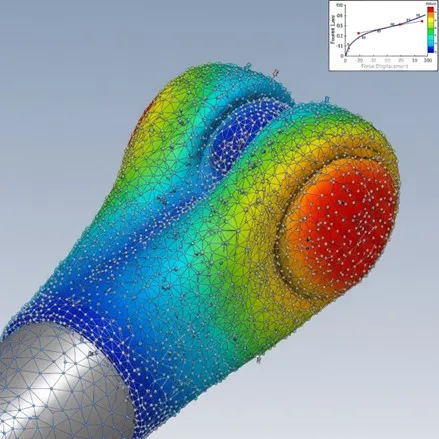
El Análisis de Elementos Finitos (FEA) es la aplicación práctica del Método de los Elementos Finitos (FEM), un procedimiento numérico que se ha consolidado como la principal herramienta de modelado virtual y simulación en la ingeniería moderna.³ Su funcionamiento se basa en el principio de “discretización”, que implica dividir un problema de ingeniería complejo y a priori irresoluble en un gran número de partes más pequeñas y manejables, conocidas como «elementos finitos».² Estos elementos están interconectados por puntos llamados «nodos» y, al resolver las ecuaciones que describen el comportamiento de cada elemento, se obtiene una solución global del sistema.⁶ Esta metodología permite a los ingenieros predecir el rendimiento estructural, acústico, electromagnético y térmico de un producto antes de su fabricación, lo que se traduce en una reducción significativa de los costos y del tiempo de desarrollo al minimizar la necesidad de costosos prototipos físicos.³

En su núcleo, el FEM para análisis estructural se basa en una relación fundamental entre fuerzas y desplazamientos, similar a la Ley de Hooke, donde una “matriz de rigidez” relaciona las fuerzas aplicadas en los nodos con los desplazamientos resultantes.⁶ Aunque esta formulación es excepcionalmente versátil y adecuada para una amplia gama de fenómenos físicos y geometrías complejas, no es la solución óptima para todos los desafíos de ingeniería. La existencia de una variedad de métodos numéricos, cada uno con una formulación matemática única, no es una redundancia. Por el contrario, es una respuesta directa y necesaria a la diversidad de comportamientos físicos en el mundo real. Por ejemplo, la simulación de fluidos, que se rige por leyes de conservación, presenta un desafío intrínseco para un método cuyo fundamento es la minimización de energía, haciendo que el FEM sea a menudo subóptimo en este campo.⁹ El objetivo de este análisis es explorar estas alternativas, ofreciendo una perspectiva integral de por qué cada método tiene un lugar vital en la caja de herramientas del ingeniero contemporáneo.

3. Desarrollo de Métodos Alternativos al FEM

Los métodos numéricos utilizados en la mecánica computacional pueden clasificarse en varias categorías que van más allá del FEM. Históricamente, se han distinguido los métodos de dominio, que discretizan todo el volumen del problema, de los métodos de contorno, que se centran únicamente en la superficie.¹⁰ Más recientemente, ha surgido una tercera categoría: los métodos sin malla, que prescinden de una malla predefinida por completo.¹³

3.1. El Método de los Volúmenes Finitos (FVM): El Enfoque de la Conservación

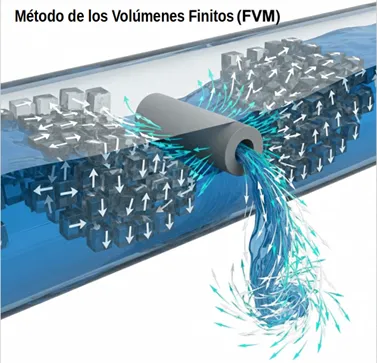
El Método de los Volúmenes Finitos (FVM) es una técnica numérica que, al igual que el FEM, transforma ecuaciones diferenciales parciales en un sistema de ecuaciones algebraicas que puede ser resuelto computacionalmente.¹⁵ Sin embargo, su principio fundamental es radicalmente distinto. Mientras que el FEM se basa en la minimización de la energía o en un enfoque de rigidez, el FVM se fundamenta directamente en las leyes físicas de conservación.⁹

Para lograr esto, el método divide el dominio del problema en «volúmenes de control» o «celdas».¹⁶ El cálculo se centra en evaluar el «flujo» de una magnitud física (como masa, energía o momento) a través de las fronteras de cada volumen.¹⁵ La principal ventaja de este enfoque es que garantiza una «conservación exacta» de la magnitud física en cada celda.¹⁵ En otras palabras, la pérdida de una propiedad en un volumen es siempre la ganancia del volumen vecino, asegurando que la conservación fundamental de masa y energía no se pierda debido a los errores de discretización, un problema común en otras formulaciones.¹⁸ Esta propiedad intrínseca lo convierte en el método preferido para la Dinámica de Fluidos Computacional (CFD).⁵

Aunque el FVM es ideal para los problemas de fluidos, presenta algunas desventajas. A diferencia del FEM, la implementación de funciones de orden superior para aproximar soluciones con mayor precisión es mucho más difícil en el FVM.⁹ Adicionalmente, la adaptación a geometrías irregulares puede ser más laboriosa que con el FEM, que está mejor equipado para manejar mallas no estructuradas.¹⁸ A pesar de estos desafíos, las aplicaciones del FVM son extensas y vitales en la ingeniería. Se utiliza en el análisis de flujo de fluidos, la transferencia de calor y la simulación de materiales viscosos.⁵ La idoneidad del FVM para CFD demuestra cómo la elección del método numérico no es arbitraria; está directamente ligada a las leyes físicas que rigen el fenómeno que se está modelando. La física de los fluidos se define por las leyes de conservación, que el FVM modela de forma natural, en contraste con la mecánica de sólidos, que a menudo se basa en principios de energía y rigidez, que son el fundamento del FEM.

3.2. El Método de los Elementos de Contorno (BEM): El Poder de la Superficie

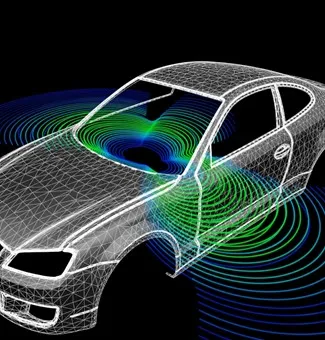
El Método de los Elementos de Contorno (BEM) representa un cambio de paradigma en la simulación, ya que reformula un problema de ecuaciones diferenciales parciales en una «ecuación integral» que solo se define en la «superficie» del dominio de estudio.¹² Esta aproximación reduce la dimensionalidad del problema, lo que significa que un problema de volumen en 3D puede ser modelado y resuelto como un problema de superficie en 2D.²⁴ Esto se logra mediante la «mallado» de la geometría solo en sus límites, no en todo su volumen interno.¹²

La principal ventaja del BEM es la simplificación masiva del preprocesamiento, al eliminar la necesidad de crear una malla volumétrica.²⁵ Este método es particularmente eficiente para problemas con una alta relación superficie/volumen o para dominios semiinfinitos, como el análisis acústico en campo libre o las interacciones entre el suelo y una estructura.¹² Al centrar los cálculos en la superficie, el BEM puede simular vastos espacios abiertos sin la exigencia computacional de mallar el volumen completo, una gran ventaja sobre el FEM en estos escenarios.²⁵

Sin embargo, el BEM no es un método de propósito general.¹¹ Su principal desventaja radica en la naturaleza de las matrices de cálculo que genera. A diferencia del FEM, que produce matrices dispersas (con muchos ceros), el BEM produce matrices «densas» y completamente pobladas, lo que incrementa exponencialmente los requisitos de almacenamiento y el tiempo de cálculo a medida que el problema crece en tamaño.¹¹ Además, es menos efectivo para resolver problemas con no-linealidades significativas ¹² y su rendimiento puede decaer en problemas interiores a frecuencias muy bajas.²⁵ Sus aplicaciones más exitosas incluyen la simulación de problemas de contacto entre sólidos ²⁸, el análisis estructural ³⁰, la acústica ²⁵, la electrostática y los problemas de vibración.²³

Una aclaración importante es necesaria, ya que la homonimia ha creado confusión en algunos contextos. El término «BEM» también se ha utilizado en el campo de la psicología para referirse a la investigación de un científico con un apellido similar. Es crucial entender que el «Boundary Element Method» de la ingeniería es un tema completamente distinto y activo en la investigación actual.¹²

3.3. El Método de las Diferencias Finitas (FDM): La Simplicidad de la Aproximación Local

El Método de las Diferencias Finitas (FDM) es el método numérico más antiguo y, conceptualmente, el más simple de los que se analizan.³³ Se basa en la aproximación de las derivadas de las ecuaciones diferenciales en una serie de puntos de una malla, utilizando expansiones de la serie de Taylor.³³

Su principal ventaja es su simplicidad.⁹ Es el método más fácil de entender e implementar en la programación. Sin embargo, esta misma simplicidad es la causa de su mayor limitación: el FDM fue diseñado para mallas de red «topológicamente cuadradas» ³³ o, en general, mallas regulares y estructuradas. Esto lo hace impráctico para geometrías complejas, ya que la adaptación a formas irregulares es incómoda y requiere mapeos globales que complican el proceso.¹¹ A diferencia del FVM, el FDM no es inherentemente conservador de masa y energía, lo que lo hace menos adecuado para la simulación de fluidos.¹⁸ Las aplicaciones del FDM se encuentran principalmente en campos como la ingeniería térmica, la mecánica de fluidos en dominios sencillos ³⁶, y la resolución de sistemas de ecuaciones diferenciales ordinarias o problemas de valor de contorno.³⁴ La rigidez geométrica del FDM fue una de las principales razones que impulsaron la evolución hacia métodos más flexibles como el FEM, que superaron esta limitación y permitieron el modelado de diseños de ingeniería complejos con mayor facilidad.³³

3.4. Métodos sin Malla (Meshfree Methods): La Nueva Frontera

Los Métodos sin Malla representan la tercera ola de innovación en la mecánica computacional, rompiendo con el requisito fundamental de una malla predefinida que conecte los nodos.¹³ Estos métodos se basan en la interacción local entre cada nodo y sus vecinos en un radio de influencia determinado ¹³, lo que los hace ideales para problemas que implican grandes deformaciones, fractura y fragmentación, donde las mallas tradicionales del FEM se distorsionan y fallan.³⁸

Dentro de esta categoría, dos subtipos son particularmente relevantes:

Hidrodinámica de Partículas Suavizadas (SPH): En este método, el continuo se discretiza en una serie de «partículas» que se mueven y transportan propiedades físicas como la masa y la densidad.¹³ Esta naturaleza Lagrangiana lo convierte en una excelente alternativa para simular el comportamiento de fluidos y sólidos bajo deformaciones extremas, como el impacto de aves en componentes de aeronaves ⁴¹ o los complejos procesos de mecanizado.⁴² El SPH es inherentemente conservador y maneja de forma natural los problemas de superficie libre, lo que le da claras ventajas sobre los métodos basados en malla en estos escenarios.³⁸
Método de Elementos Discretos (DEM): A diferencia de los métodos de continuo, el DEM modela materiales particulados, como granos, arena o polvos.³⁹ El método trata cada partícula como una entidad distinta y representa el material a granel como un conjunto idealizado de partículas.⁴³ El DEM es la herramienta ideal para simular el flujo de materiales a granel, el desgaste de equipos en la agroindustria y la minería, y para optimizar el transporte y almacenamiento de materiales granulares.⁴⁴ Permite una comprensión del comportamiento a nivel de microescala que no es posible con métodos de continuo como el FEM.⁴³

Las principales ventajas de los métodos sin malla son su capacidad para simular de forma precisa fenómenos de fractura y grandes deformaciones sin los problemas de distorsión de la malla del FEM, y la eliminación de la laboriosa tarea de mallado en el preprocesamiento.³⁸ Sin embargo, su principal inconveniente es el alto costo computacional.⁴⁰ Además, la imposición de condiciones de contorno puede ser más compleja que en el FEM.¹³ La aparición de los métodos sin malla demuestra cómo la naturaleza del problema físico, y no solo la optimización geométrica, impulsa el avance tecnológico en la mecánica computacional.

3.5. Enfoques Híbridos y Acoplamientos: Lo Mejor de Ambos Mundos

La continua evolución de los métodos de simulación ha llevado a una conclusión crucial: la ausencia de un «método superior» universal. La verdadera sofisticación de la simulación moderna reside en la capacidad de combinar las fortalezas de diferentes enfoques en un solo modelo. Los acoplamientos entre métodos son la manifestación más clara de esta tendencia.⁵

Un ejemplo destacado es el acoplamiento de SPH y FEM. En simulaciones de mecanizado, la zona de alta deformación donde se forma la viruta se modela con el método SPH para capturar la deformación extrema y la fragmentación.⁴⁰ Simultáneamente, el resto de la pieza de trabajo, que experimenta deformaciones menores, se modela con el método FEM para aprovechar su alta eficiencia computacional.⁴² Este enfoque híbrido ha demostrado ser capaz de reducir el tiempo de simulación hasta en un 40% sin sacrificar la precisión, lo que representa una ganancia significativa.⁴²

De manera similar, el acoplamiento FEM-BEM es común en el análisis acústico, donde el BEM se utiliza para modelar la propagación del sonido en el dominio infinito de aire y el FEM se aplica a la estructura vibrante.²⁵ Este enfoque de coexistencia optimiza el rendimiento y la precisión de la simulación. La capacidad de combinar inteligentemente diferentes métodos es una respuesta directa a los desafíos de «complejidad, precisión y escalabilidad» ⁴⁸ que enfrentan los ingenieros.

Tabla 1: Comparativa de Métodos Numéricos Clave

Método	Principio Físico/Matemático	Aplicaciones Típicas	Ventaja Principal	Desventaja Principal
FEM	Minimización de Energía	Estructural, Térmica, Electromagnética	Manejo de geometría compleja	Puede tener problemas con fluidos y grandes deformaciones
FVM	Conservación de Flujos	Dinámica de Fluidos Computacional (CFD), Transferencia de Calor	Conservación de masa y energía inherente	Dificultad con geometrías complejas no estructuradas
BEM	Ecuación Integral de Contorno	Acústica, Electrostática, Contacto	Reduce la dimensionalidad del problema, ideal para dominios infinitos	Matrices densas, lo que incrementa el costo computacional
FDM	Aproximación de Derivadas	Ingeniería Térmica, Mecánica de Fluidos en dominios simples	Conceptual y computacionalmente simple de implementar	Restringido a mallas regulares y estructuradas
SPH	Partículas Lagranigianas	Grandes Deformaciones, Fluidos de Superficie Libre, Impactos	Ideal para fractura y deformaciones extremas	Alto costo computacional
DEM	Cuerpos Discretos Rígidos	Flujo de materiales granulares, Interacción Partícula-Estructura	Simula el comportamiento de materiales a microescala	Alto costo computacional

4. Líneas de Investigación y Futuras Tendencias

El futuro de la simulación no se limita a la mejora incremental de los métodos existentes, sino que abarca una revolución impulsada por la convergencia de la inteligencia artificial (IA), el aprendizaje automático (ML) y la computación cuántica.⁷ Estas tecnologías emergentes prometen cambiar el paradigma de la simulación de ingeniería.

La inteligencia artificial y el aprendizaje automático se están integrando para acelerar los cálculos, optimizar automáticamente los modelos y automatizar tareas de preprocesamiento que consumen mucho tiempo.⁷ En un futuro cercano, se espera que la IA «agéntica» tome decisiones autónomas sobre la elección del método de simulación más adecuado o la combinación óptima de métodos para un problema dado, democratizando así el acceso a la simulación.⁴⁹

La computación cuántica, por su parte, promete resolver problemas de simulación masivos que son intratables para los ordenadores clásicos, lo que podría revolucionar áreas enteras de la ingeniería, desde la investigación de nuevos materiales hasta el diseño de sistemas complejos.⁵⁰

Finalmente, la integración de estos avances en la tecnología de los «gemelos digitales» transformará la simulación en una herramienta que no solo predice, sino que interactúa en tiempo real con sus contrapartes físicas.⁵⁰ Un gemelo digital es una réplica virtual dinámica de un producto o proceso que se beneficia del aumento en la potencia y la precisión de los métodos de simulación. Estas futuras tendencias apuntan a un cambio fundamental en el que la simulación dejará de ser una tarea aislada para convertirse en un ecosistema inteligente y omnipresente en el ciclo de vida completo de un producto.

5. Conclusiones

Este análisis ha demostrado que la elección del método de simulación óptimo en ingeniería mecánica es una decisión informada que depende de la naturaleza específica del problema. Mientras que el Método de los Elementos Finitos es una herramienta versátil y universalmente adoptada, existen alternativas especializadas que ofrecen soluciones superiores para ciertos desafíos. El Método de los Volúmenes Finitos es el líder indiscutible para la Dinámica de Fluidos Computacional, gracias a su enfoque inherente de conservación.⁹ El Método de los Elementos de Contorno es ideal para problemas de dominios semiinfinitos o con alta relación superficie-volumen, como en la acústica de campo libre.²⁵ Por su parte, los Métodos sin Malla, como el SPH y el DEM, han surgido como la solución definitiva para problemas de grandes deformaciones y materiales granulares, respectivamente.³⁸

El futuro de la simulación de ingeniería no reside en la supremacía de un solo método, sino en la capacidad de combinar y acoplar inteligentemente estos enfoques para resolver problemas multifísicos y complejos de manera más eficiente y precisa.⁴² La IA y la computación cuántica no buscan reemplazar los métodos numéricos existentes, sino potenciarlos, transformando la simulación de una disciplina técnica en un ecosistema predictivo e indispensable para la toma de decisiones en todos los campos de la ingeniería. La verdadera ventaja reside en la habilidad de seleccionar y fusionar las herramientas correctas para cada desafío, marcando el camino hacia una nueva era de la ingeniería computacional.