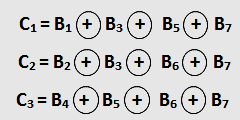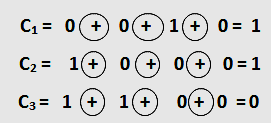Sistema Combinacional o Lógica Combinacional (Parte 1)
Autor: Rubén San Martín – Centro de Ingeniería Eléctrica y Sistemas (CESICE). FIIIDT.
El término Sistema Combinacional o Lógica Combinacional se le da a todo Sistema Digital en el que sus salidas son función únicamente del valor de sus entradas y una operación entre ellas, ocurriendo en un momento dado, sin que sean influenciados por la condición de los estados anteriores tanto para las entradas como para las salidas. Las funciones lógicas son utilizadas en el algebra Booleanas (OR, AND, NAND, XOR), donde cada función se la asigna una función específica y se puede representar en una tabla de la verdad. Por su naturaleza no posee retroalimentación ni memoria. [1]
La lógica combinacional está formada por ecuaciones simples a partir de operaciones básicas del Algebra de Boole. Un circuito combinacional es aquel que está formado por funciones lógicas elementales que tiene un número de entradas y otro número de salidas, y los valores de éstas dependen exclusivamente del estado que adopten las entradas y de su constitución interna. Los Circuitos Combinacionales de Media Escala de Integración (MSI) poseen entre 10 y 100 compuertas, esto equivale a un total entre 100 a 1000 transistores integrados en una pastilla o encapsulado.
Los circuitos combinacionales de Media Escala de Integración se clasifican en dos grupos según la función que desempeñan en el interior de los Sistemas Digitales: Circuitos de Comunicación y Circuitos Aritméticos.
Los Circuitos de Comunicación, sirven para transmitir información por una línea como para codificar, decodificar o modificar la estructura de dicha información. Los más utilizados son: Los Codificadores, Los Decodificadores, Convertidores de Código, Multiplexores y Demultiplexores. [2]
Los Circuitos Aritméticos, estos realizan una serie de operaciones aritméticas con los datos binarios que procesan. Los más importantes son: Comparadores, Sumadores y Restadores.
Cualquier información que se desee tratar, procesar o almacenar mediante Sistemas digitales, deberá ser traducida o Codificada en un tipo de lenguaje apropiado. La forma correcta de hacerlo es convertir cualquier número, letra, signo, instrucción u operación en un conjunto de señales eléctricas digitales, que será diferente en cada caso. Cada uno de estos datos estará constituido por una serie de unos (1) y ceros (0) que indicarán niveles altos o bajos de tensión respectivamente. Por ejemplo, el número 9 en decimal, se puede representar por 1001, el cual es su equivalente en el sistema binario. De la misma forma, a la hora de interpretar un resultado a la salida de un circuito digital, es necesario traducir o Decodificar el resultado transformando los ceros y los unos en datos que sean inteligibles.
La Codificación y la Decodificación serán siempre operaciones necesarias en sistemas digitales que traten información, o en procesos industriales donde sea necesario suministrar datos o presentar resultados.
Es importante saber y entender qué es un Código, en general, es un conjunto de unidades de información relacionadas de forma sistemática y biunívoca con otro conjunto de signos y símbolos según unas determinadas reglas de traducción previamente fijadas. Los códigos más comunes utilizados son: El Binario Natural, el Decimal Codificado en Binario (BCD-Natural, BCD-Exc 3 y BCD-Aiken), los códigos Progresivos, los códigos Detectores y Correctores de Error y los códigos Alfanuméricos.
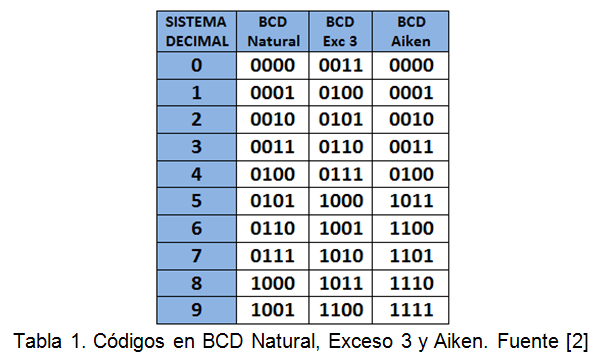
Los códigos BCDson los más utilizados para representar información numérica. Para codificar un número decimal en BCD, se representan por separado cada una de las cifras del número. Cada cifra se representa mediante 4 bits. En BCD Natural, se utilizan las diez primeras combinaciones en orden creciente, en BCD Exceso 3, no se utilizan las tres primeras, ni las tres últimas y en BCD Aiken, se emplean las cinco primeras y las cinco últimas. La Tabla 1 muestra la Equivalencia entre los diferentes Códigos BCD.
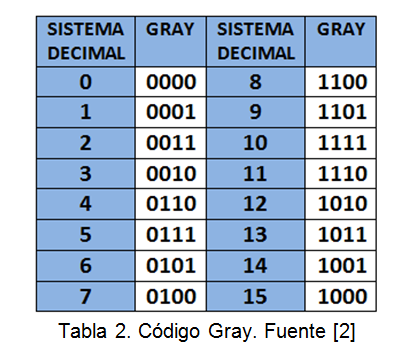
Códigos Progresivos,la característica fundamental es que una combinación difiere de la anterior y de la siguiente exclusivamente en un solo bit. Se emplean en procesos industriales para transformar magnitudes físicas analógicas en digitales. Los más utilizados son los de Gray. La diferencia entre unos y otros reside en el número de bits de cada combinación.
Códigos Detectores y Correctores de Error, existen códigos más complejos que detectan y en algunos casos corrigen, el error en la información cuando ésta es transmitida a través de una red. El error se detecta o corrige si se produce en un solo bit de la combinación. La posibilidad de que se origine en dos bits a la vez es muy remota. El número mínimo de bits por combinación es de cinco.
Los códigos detectores más comunes son los de Paridad o 2/5 y 2/7 o biquinario. Los dos últimos están formados por combinaciones de 5 y 7 bits respectivamente, siendo dos el número de unos lógicos en cada combinación en ambos casos.
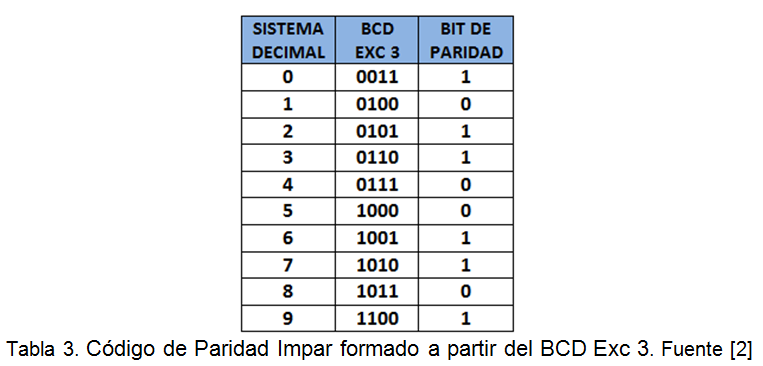
Los Códigos de Paridad se forman añadiendo un bit más a los de la familia BCD. Pueden ser de Paridad Par o de Paridad Impar. En el primer caso el número de unos, incluido el de paridad, debe ser par y en el segundo impar.
La Tabla 3 muestra el Código de Paridad Impar formado a partir del BCD Exc 3.
El Bit de Paridad se genera mediante un circuito combinacional muy sencillo, llamado Generador de Paridad que se construye con Compuertas OR-Exclusive. La detección se realiza comprobando que el número de “unos” en cada combinación es siempre par o impar, según el caso.
Los Códigos Correctores proporcionan el lugar que ocupa el bit erróneo. Mediante el circuito adecuado se puede corregir automáticamente el fallo detectado en la información recibida. Se utilizan en procesos industriales.
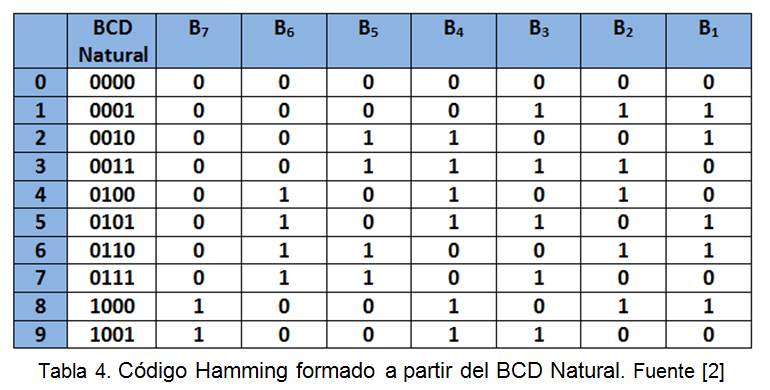
El código corrector más utilizado es el HAMMING. En el cual cada combinación está formada por siete bits y para su construcción se parte de la familia BCD. La Tabla 4 muestra el Código Hamming formado a partir del BCD Natural.
Los siete bits están relacionados mediante las siguientes ecuaciones:
El número decimal equivalente a la combinación binaria C3 C2 C1 indicará el bit con error. Las columnas B7, B6, B5 y B3 corresponden al BCD Natural. Las columnas B1, B2 y B4, se construyen de manera que en cada combinación: B1 B3 B5 B7, B2 B3 B6 B7 y B4 B5 B6 B7, los números de “unos” sea par. Cuando no existe error, el valor de las funciones C1, C2 y C3 será cero.
Para comprender la forma de operar, supongamos que al transmitir el número tres cuyo valor codificado es 0011110 se produce un error y la combinación recibida es la 0011010. El valor de C1, C2 y C3 será:
La combinación C3 C2 C1será en este caso 011, que equivale al número tres decimales. El bit equivocado es el tercero por la derecha.
Esta primera parte se centra en la explicación teórica de los Sistemas Combinacionales y la comprensión de los diversos códigos en binario para la transmisión de datos, es importante comprenderlos para más adelante, en la segunda parte de esta nota técnica, sea más sencillo comprender todos los circuitos de comunicación tales como Los Codificadores, Los Decodificadores, Convertidores de Código, Multiplexores y Demultiplexores.
Bibliografías:
[1] Blogspot Circuitos Lógicos (2012). Lógica Combinacional. Fecha de consulta: 29, septiembre, 2020 desde https://albelisv.blogspot.com/2012/05/logica-combinacional.html
[2] Andrés Herrera (2016). Trabajo de Laboratorio Nº02: Diseño de Sistemas Lógicos Combinacionales en Media Escala de Integración (MSI). – Venezuela (Guía de Laboratorio de Sistemas Lógicos) Charallave: Universidad Nacional Experimental Politécnica “Antonio José de Sucre”, Ingeniería Mecatrónica.
Contacto: rubensanmartin95@gmail.com